A Researcher Shores Up Einstein’s Theory With Math

In 1915, in a series of lectures in Berlin, Albert Einstein introduced his theory of general relativity, using an equation to demonstrate that energy and matter affect the shape of space-time, causing it to curve. In 1963, the mathematician Roy Kerr solved the equation that Einstein had introduced in 1915 with a proof that described the space-time outside of a rotating black hole. In the decades since, researchers have tried to prove that the black holes that Kerr found are stable, or as the writer Kevin Hartnett put it in a 2018 Quanta article that if you jolt one it “shakes like Jell-O then settles down into a stable form like the one it began with.” 
 
This spring, Professor Elena Giorgi proved exactly that. In a 900-plus-page paper that she co-authored with fellow mathematicians Sergiu Klainerman, of Princeton University, and Jérémie Szeftel, of Sorbonne University, Giorgi demonstrated that black holes are indeed stable. Had she and her fellow researchers found that black holes were not stable, it would have raised a host of problems for physicists, Giorgi said, and could have suggested that Einstein’s theory of general relativity was wrong.
 
Giorgi, who is originally from Italy, earned her PhD from Columbia in 2019. She spent two years at Princeton as a postdoctoral research associate before joining Columbia as an assistant professor in July of 2021. Columbia News caught up with Giorgi to learn more about her work on black holes and what her solution means for the field.

Can you sum up why the findings from your recent paper are so important?

What we demonstrated is the stability of this black hole that Kerr solved for when it is slowly rotating. Now, I'm a mathematician; we're in the math department. So why are we even talking about black holes? Because those objects are really a mathematical solution to Einstein’s field equation, which he introduced in 1915, when he discovered the theory of gravity. It's what made it possible for Einstein to go from his theory of special relativity, where there is absolutely no matter in the picture, to understand how it would operate in our universe where there are massive objects like stars. What I study is the mathematical properties of black holes. People who do physics and astrophysical observations and so on use these mathematical solutions to do their computations.

Why is it important for black holes to be stable?

Let’s take the example of a pendulum. A pendulum’s point of equilibrium is when it is facing down; you can oscillate it, but it always returns to that position.

But if you analyze the pendulum from a mathematical point of view, it actually has two points of equilibrium, points where it stays perfectly still and doesn’t oscillate. One is when it's downward. But the other point is when it’s upward, facing in the exact opposite direction with the pendulum’s weight 180 degrees above where a pendulum would normally hang. If you were able to put it exactly in its vertical position, it would remain there, it would not move. But of course, you know, I’ve never seen a pendulum in this position and the reason why I have never seen it is because it’s an unstable point of equilibrium. If you move it a little bit, it will fall down and start oscillating around its stable, downward point of equilibrium.

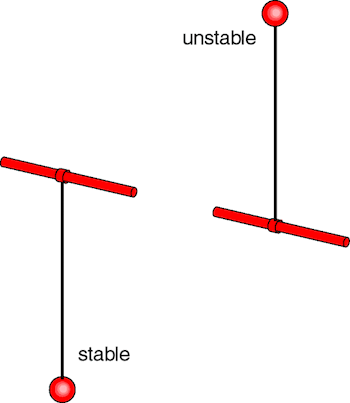
Wouldn’t it be able to stay directly upright if you used your hand to move it around and keep it balanced?

That’s different, because then you would be adding a lot of dynamics to the pendulum to keep it balanced in that vertical position.

The idea of stability is crucial in physical and mathematical objects such as the pendulum because the difference between being stable and unstable is the difference between something that is feasible and not feasible. It's unfeasible to find the pendulum in that upward position. Because in fact, we are never able to position the pendulum exactly in the upward position, because we will always have some error in positioning it. It can only be posed in our mind as a point of equilibrium, but not in the real world.

And how does that connect back to black holes?

Black holes are solutions to the Einstein equation, and they are the point of equilibrium for the Einstein equation. The Kerr solution came out in 1963, many years after Einstein’s equation was written down in 1915. That solution finds a point of equilibrium with Einstein’s equation that doesn’t change over time. But then the question is: Is that a pendulum facing down or a pendulum facing up? Because if it’s a pendulum facing up, then it’s a nice solution, but it can’t represent anything in the real world.

The physics community performed stability analysis for these black hole solutions in some simplified settings and did not find any sign of instability, so they deduced that black holes are stable, without really proving it. But it took about 60 years or so for the mathematics community to catch up and understand what the actual mechanism for this is.

Could we have assumed black holes were stable just by looking at them and observing that they do exist?

It's a very good question but observing black holes is not as simple as, you know, observing a cat. The way that images of a black hole are produced is that there’s an image captured by telescopes, but there’s also a blueprint that uses the Kerr solution. How do you interpret the data you see? By comparing it with your model. Some things are deduced by observation and others are assumed based on mathematics.

Were you always interested in outer space? Or did you come to it because phenomena in outer space posed the most interesting mathematical problems?

I studied mathematics in undergrad when I was in Pisa in Italy, and then I did a master's in mathematical physics in France. Since high school or even before that I always liked mathematics and physics, so I was looking for something that would bring them together.

And then, of course, black holes: Who doesn’t think they’re fascinating?

The month I started a PhD, which was September 2015, was when the LIGO’s first observation of gravitational waves happened. It was announced in February 2016. [That year, two observatories in Louisiana and Washington known as LIGO detected gravitational waves, ripples in space-time that Einstein’s theory predicted would occur, proving the veracity of his predictions.]

I was here. I was a student at Columbia and I remember I went to Lerner Hall, they projected the discovery of gravitational waves in February 2016. It was so exciting. Maybe it was a kind of destiny. This observation gave a big boost to the field, making it feel much richer than if you didn't have these observations. Some other areas of physics, like string theory, don't have these kinds of waves of data coming in from real observations.

What brought you to Columbia specifically?

I did my master’s in France, so I was already abroad in a certain sense. And I felt like I wanted to go somewhere else again. I always wanted to have an experience in the U.S., for example. I applied for PhDs very broadly. And I had some admission offers and then I visited Columbia and I was in New York. It was very hard to say no, it was so exciting. They showed me around the department and being in the city, with other students, I was convinced very quickly. Also because of the people here working on differential geometry and general relativity, Columbia made a lot of sense.

Do you feel like you follow developments from NASA and other space agencies particularly closely?

Not really. On a personal level, I love it, of course; I get all the newsletters. But those aren’t directly relevant to the work I do. I’m not a big stargazer.

The field of mathematics skews very male. Did you have strong female mentors coming up in the field? Do you see that as a role you want to play for young women mathematicians?

Mathematics indeed tends to be very male-dominated. Just to give an example, our department has only four full female professors out of 29, and there are other departments in the country where the ratio is even worse. I believe that having mentors you can relate to is very important, as it helps to nurture a sense of belonging when you are a student. I have been lucky to have been exposed to amazing scholars during my years as a graduate student at Columbia, who showed me different ways of being a mathematician. For my part, I can only hope to have a positive impact on younger people who are passionate about mathematics and physics, and I do my best to let them feel like they belong to this field. Because they do.

What do you miss the most about home, foodwise? 

What I miss the most is ice cream, gelato. Here you can find some, but it’s downtown, or in midtown, and very expensive. But for pizza, I think I can find even better pizza here than in Italy.